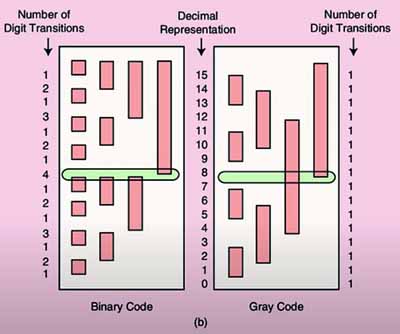
Le codage (tube de conversion parallèle ou tube à sortie série sans asservissement) n'est pas un codage binaire classique dont les valeurs sont 000, 001, 010, 011, 100, 101, 110 et 111 mais un codage de Gray. Dans ce code, la différence entre deux valeurs consécutives est toujours représentée par le saut d'un seul bit (distance de Hamming = 1). Dans le cas d'un codage binaire classique, les sauts de Hamming (nombres de bits qui changent) sont les suivants:
000 [1] 001 [2] 010 [1] 011 [3] 100 [1] 101 [2] 110 [1] 111.

Je ne vais pas entrer dans les détails, mais ce code permet d'élimimer les erreurs à la lecture.

Il n'a pas un seul code de Gray, mais plusieurs codes. Le code binaire réfléchi est construit de telle manière que le passage de la valeur binaire la plus élevée à la valeur la plus basse produit également une modification d'un seul bit. Ce code n'est pas nécessaire dans notre exemple, mais peut par exemple être utilisé sur un encodeur rotatif. Les codes montrés ici sont des codes réfléchis.

L'exemple à 4 bits montre ce qui peut se produire dans une situation extrème où les 4 bits changent simultanément et le rayon frappe la cible entre deux valeurs. La valeur qui est effectivement lue peut prendre n'importe quelle valeur de 0000 à 1111: la valeur qui est lue n'est pas définie, alors que la valeur analogique se situe entre 7 et 8.

Avec un système de Gray, la numérisation ne peut produire qu'une valeur 7 (codée 0010) ou 8 (codée 0011). La marge d'erreur est donc réduite à l'erreur de numérisation. Ce système est actuellement encore utilisé dans de nombreux domaines.

Dans le code de Gray, il n'est pas possible de déterminer le poids d'un bit et il est impossible de faire des calculs avec ce code. De plus, il n'existe pas un seul code de Gray, mais plusieurs codes sont possibles.

Le code est dit "réfléchi" (reflected) can il peut être construit récursivement pour un nombre de bits donné en partant de deux bits qui sont étendus:
00 01 11 10 deux bits de base
10 11 01 00 réflection
000 001 011 010 110 111 101 100 ajout d'un 0 ou d'un 1 et concaténation
Nous avons maintenant un code à 3 bits et la procédure peut être répétée autant de fois que nécessaire.

Comme vous pouvez le lire sur la page des systèmes de conversion analogique - numérique, une vitesse de conversion élevée produit une précision moindre (pour une complexité du système identique).

Ces systèmes ont atteint leur apogée vers 1965, au moment où les premiers circuits intégrés sont apparus sur le marché. Un convertisseur 'solid state' avec des caractéristiques identiques nécessitait une centaine de circuits élémentaires (comparateur, fonction AND, OR, XOR,...) montés sur une dixaine de plaquettes. Le coût du convertisseur solid state était moindre et les convertisseurs basés sur un tube à rayon cathodique ont rapidement disparu.

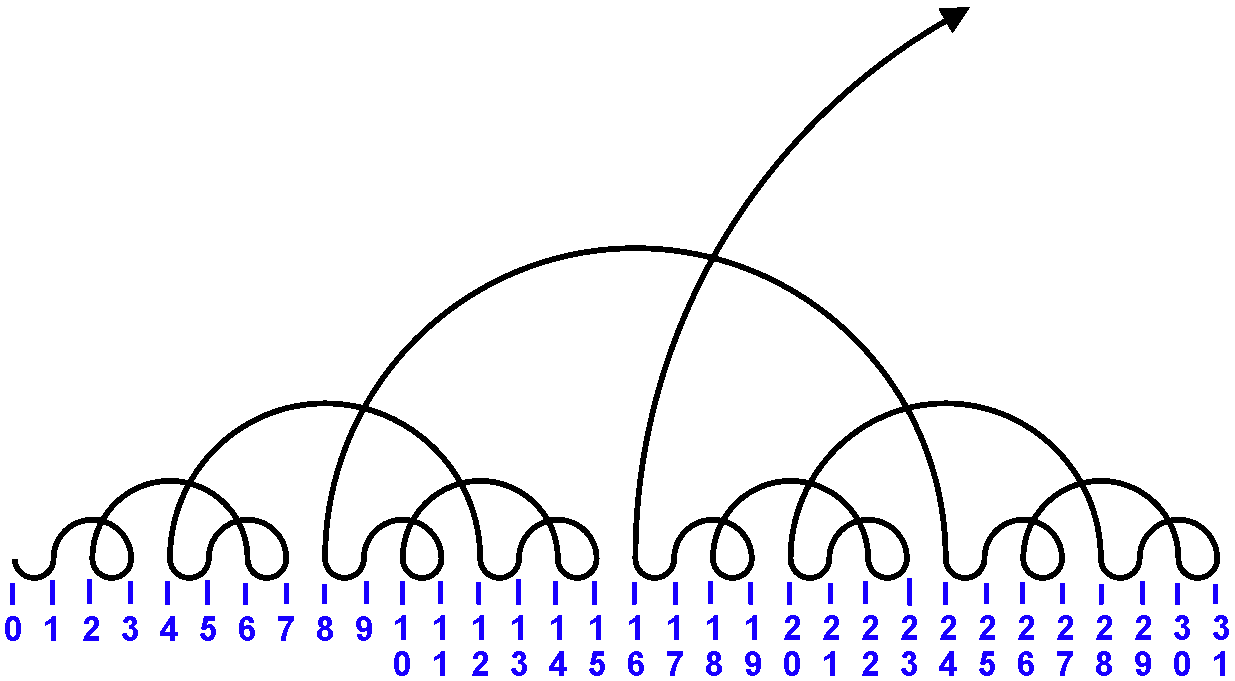
La représentation à droite montre la progression d'un nombre binaire réfléchi: en binaire normal la progression est de 0 1 3 2 6 7 5 4 12 13 15 14 10 11 9 8 ....

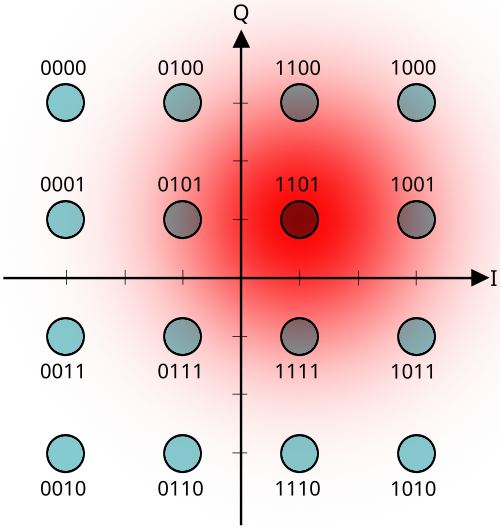
Ici aussi le passage d'une position à une autre se fait par le basculement d'un seul bit à la fois, tout comme le passage de la position maximale à la position minimale.

Si l'encodeur rotatif semble un système tout simple, la seconde application est beaucoup plus pointue. La transmission des données utilise toujours une modulation, ce qui permet de transmettre des données en utilisant une bande passante définie à l'avance. Plusieurs communications peuvent également être transmises à la fois.

La modulation a été utilisé pour la première fois sur le réseau téléphonique pour connecter deux ordinateurs à distance, mais est maintenant également utilisé avec les téléphones portables, la communication vers les satellites. C'est toujours me même principe, mais le hardware a été amélioré.

La modulation la plus souvent utilisée est la modulation QAM (quadrature-amplitude modulation et merde la traduction en français) qui permet de transmettre 16 bits par baud. Cette modulation a été lancée quand on utilisait encore des lignes téléphoniques normales dont la bande passante ne monte qu'à 3000Hz (un modem "normal" avait un débit de 2400baud). En utilisant une modulation QAM-16 on augmente la bande passante à 38.4kb/sec.

Mais ce qui est important, c'est que chaque constellation a des voisins qui ne diffèrent que d'un bit. S'il y a une erreur dans le décodage, l'erreur ne concerne qu'un seul bit. Dans notre cas la valeur transmise est 1101, en cas de mauvaise transmission le code reçu est 1100, 1001, 1111 ou 0101.

Cette différence d'exactement un bit peut facilement être détectée par l'ajout d'un bit de parité, et dans les systèmes plus évolués peut même être corrigée automatiquement. Et c'est pour cela, mon cher, qu'on utilise toujours le codage de Gray.

Pour la petite histoire, les français sont les seuls à utiliser le nom de code de Gros-Gray et non pas le code Gray comme tout le monde. Ils ont été chercher dans l'histoire ancienne un type qui a pondu un jour de pleine lune un article sur le sujet (mais sans en exploiter les possibilités, qui étaient inexistantes à l'époque). Et c'est pour cela que le fil à couper le beurre est appellé fil Charlemagne en France; l'eau chaude est appellée eau normande; le canon, tuyau français; le sonar, écho corse; le polonium (Po), Pompidium; la roue de vélo de course, poulie d'or (seuls les plus agés comprendront); la lampe à incandescence, la bougie française; et ainsi de suite...